
Can We Quantum Tunnel Through A Wall?
Quantum mechanics defies all intuition about our perceptible classical universe. The simple act of measuring a particle's position and then its momentum doesn't yield the same result as measuring the momentum first and then the position. This is a reflection of Heisenberg's uncertainty principle. The more we try to sharpen our knowledge about the particle's position, the muddier our understanding of its momentum gets.
What’s even stranger is that in the quantum world, particles are not confined to a single spot; their position is described by a wavefunction encoding the probability of finding it at some position. This wavefunction does not end abruptly anywhere in space; it decays exponentially, never reaching zero. If the wavefunction "leaks" through a barrier (or a wall), there's a non-zero chance of it appearing on the other side. This gives rise to the phenomenon of quantum tunneling, which is when a quantum system can cross barriers that are forbidden classically. In this article, we demystify quantum tunneling in simple terms and give reassurance to those wondering if they might instantaneously tunnel through a wall.
The Quantum Wavefunction
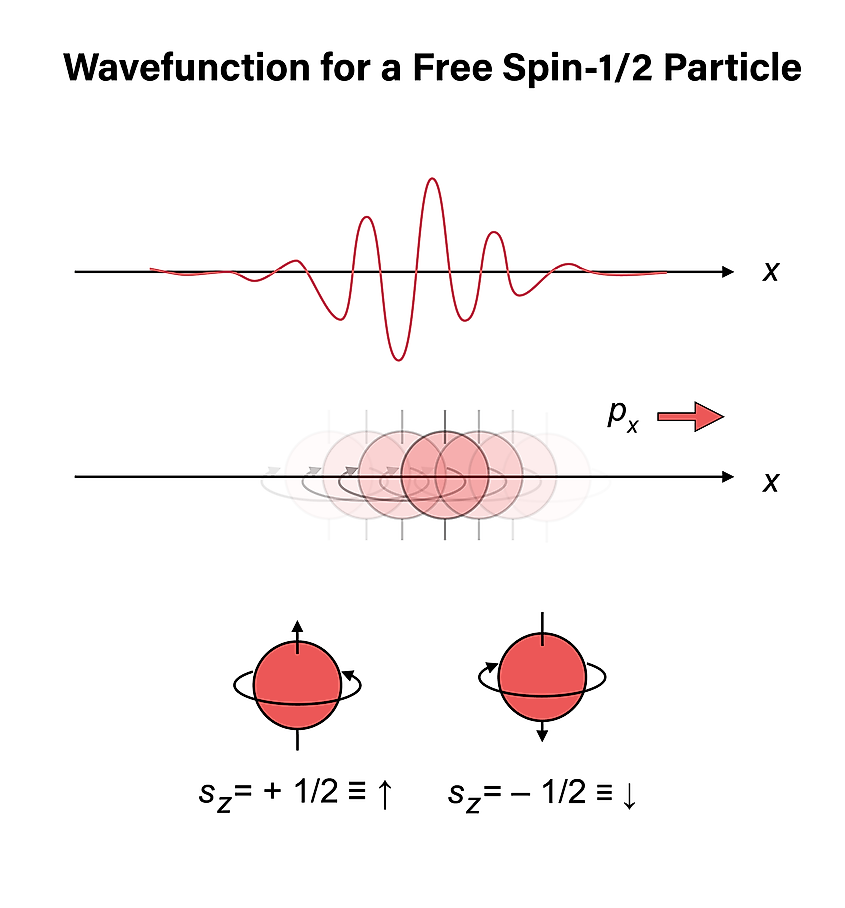
Quantum theory differs fundamentally from classical theory in many ways. The most basic way is that quantum mechanics is a theory of probability amplitudes, while classical mechanics is one of probabilities. Amplitudes are essentially square roots of probabilities, but weirdly, they can take on imaginary values. In classical theory, we can ask what the probability of observing the particle in one position or another is. The total probability of finding the particle in either position is simply given by the sum of the individual probabilities. Life is good.
In quantum theory, the probability of finding the particle in either position is the square of the sum of the amplitudes. When we square two terms, we get mixed terms that signal quantum interference. This is radically different from classical theory, in which those mixed terms do not exist.
To describe a system in quantum mechanics, we simply put all the probability amplitudes for finding it somewhere in what we call the wavefunction. This is in opposition to classical theory where the system can be described by a probability distribution. One can think of the wavefunction as a probability amplitude distribution.
Barriers, Potentials, and Walls
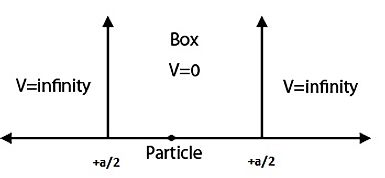
The quantum description of a free particle is simple. Depending on its momentum, there will exist some probability of finding the particle in some position dictated by how heavy it is and how fast it is moving. The wavefunction which is sharply peaked at some position (momentum) is not valid which is a reflection of uncertainty.
To make life more interesting, we can imagine placing the particle in a well. Now, there will exist different regimes for the description. The particle can have:
- Energy less than that of the well (or barrier), in which case it is seemingly trapped and cannot escape.
- Energy greater than that of the well, in which case it does not even register the barrier and behaves as if it were freely propagating.
- Energy equal to that of the well, in which case it can go either way.
An example of a well could be the trapping Coulomb potential of an electrically charged nucleus applied to the quantum description of an electron in an atom. Depending on the charge of the nucleus, the electron may or may not be trapped by the potential.
Surpassing Obstacles and its Consequences
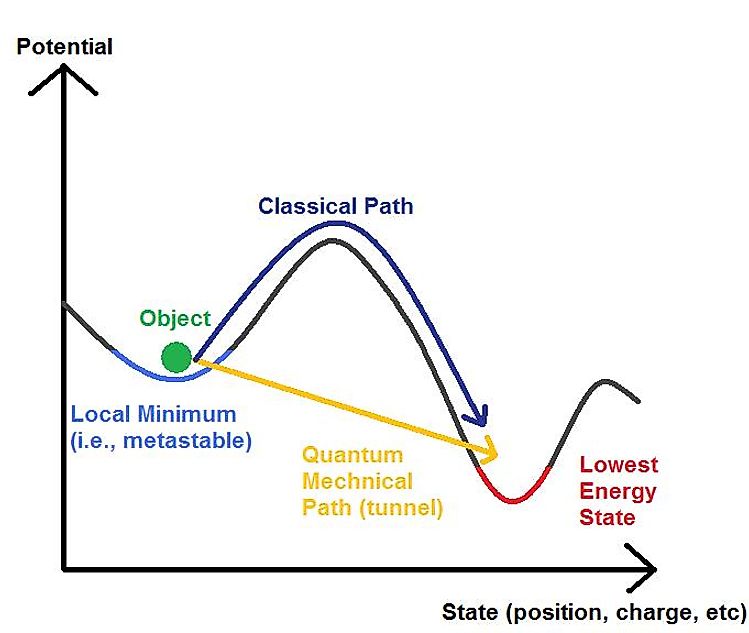
Let us imagine that we have a particle in a finite box. In classical theory, if the particle does not have enough energy to climb the walls of the box, then it will simply stay inside forever. Only if its energy is greater than that of the trapping potential can it ever escape. In quantum theory, this is no longer true!
To understand why, we recall that the wavefunction is supported in any position in space. This means there is a non-zero probability of finding the particle outside of the box independently of its energy. The probability, of course, does depend on the energy, but the fact that it can be outside does not. This is exactly what quantum tunneling means. The surprising thing about this is that it defies our classical expectation. Even if classically, the particle is forbidden from escaping, quantum effects can save the particle from its fate.
Why is this important? Tunneling is essential for many fundamental processes like:
- Nuclei in stars can overcome their electric repulsion via quantum tunneling, which enables fusion reactions to occur. These fusion reactions are important to sustain the star. Without tunneling, our Sun would not exist.
- Tunneling also governs some radioactive decay channels. For example, alpha decay, which is the ejection of a Helium nucleus from a decaying parent nucleus, would not occur without tunneling. Without this process, some cancers would not have been able to be treated or pacemakers made.
- Bodily processes rely on enzymes, which catalyze reactions that lead to digestion and respiration. If the protons and electrons found in enzymes could not tunnel, the reactions would occur too slowly to sustain life itself.
While tunneling is extremely important for many aspects of life, it is important to remember that quantum effects become heavily suppressed when we consider bigger systems. This is why, for the electron, tunneling is commonplace, while for humans, trying to get past a locked door, not so much.











